I wanted to share with you in this post a speech I gave last Saturday at Rosemasters club contest. I was not contesting but a speech was needed for the evaluation contest, so I volunteered.
Why do I share this speech in particular? Not because it was especially good (nor especially bad), but because it has some insights that could help some of you in case you hadn’t reflected on them or made the numbers yourself.
I titled the speech “Snowball” but a more suitable title would have been “Snowball, or the beauty of compound interest”. Please, note that the metaphor of the snowball it’s not mine, so no need to praise my originality here. I borrowed it from Alison Schroeder’s biography of Warren Buffett “Snowball”, which I reviewed in other post in this blog (I take the opportunity to recommend the book again).
Below you can watch the video uploaded in Youtube (from the second 0:42 some helping hand lifts the camera, please be patient during those first seconds). Below the video I share the script of the speech so you can actually see the formula and the charts I showed. Reflect on it; it may help you a lot a long way down the road.
—–
Script:
“How many of you used to play with snow when you were a child?
Do you remember what the process you followed to build snowballs was? You started by making a small ball with your hands, like this. Then, you left it on the ground and let it roll over itself, so it was gaining more snowflakes and thus getting a bit bigger with every roll… for you it was a small effort, and after some time of rolling and rolling over, you easily could end up with big snowball like this.
Mr Contest chair, fellow members and guests,
Today I haven’t come to talk about snow. I want
- to explain the concept of compound interest
- to show how important it can be for or future and
- maybe to persuade you to take some action.
Let’s start:
This is the formula.
It shows what is the future value (FV) of an investment’s present value (PV) that gains a fixed interest rate (i) for n periods.
To put it simple, it means that the interest that we earn over the investment in the first year, will enter the calculation in the second year. In a very similar way that small snowflakes are making the snowball bigger.
- The importance of compound interest for our future.
Who is the younger member of the audience today? I will ask you one question, let me see if I get the answer I want.
Are you saving and investing with your retirement in mind? Do you have pension plan or fund?
An extremely important factor in this discussion is that time in the formula appears in the exponent. This means the longer the time period, the better. Or put it in another way, the sooner we start investing or saving, the better.
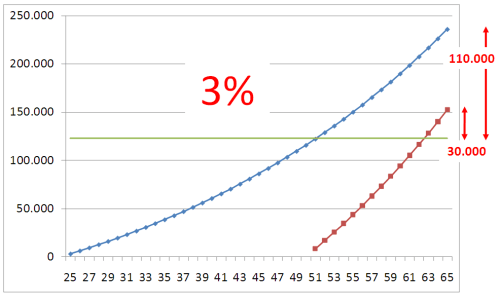
I made two quick calculations to show you. Imagine a 25 year old person who just started working. If he or she is able to save 250 euros per month, that is 3,000 euros per year, and puts it in a conservative fund which earns 3% a year… by the time he is 65 he will have around 230.000€. His yearly contribution would have been 123.000€. So another 110.000€ will have come from the interest. He will practically have doubled his money.
On the other hand, take a 50 year old person who never saved any money beforehand. He will have to save it in only the last 15 years of his working life. To make the comparison, I supposed that he contributed the same 123.000€ in those 15 years, for this he has to save 8.200 per year or 680€ per month… when he is 65 he will have 150.000€, having earned about 30.000€ from the interests, 4 times less!
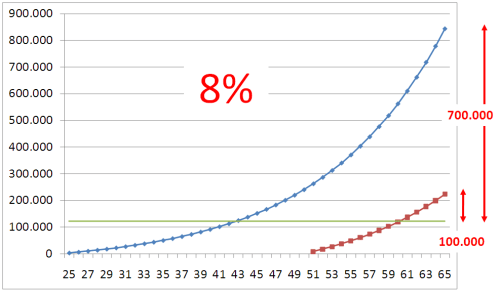
If the young person would invest in more volatile asset, for example the stock market, which historically earns about 8% every year, the new figures would be these ones.
- 840.000 – earning 720.000 from interests
- 222.000 – earning 100.000 from interests / 7 times less.
Finally, with this discussion I wanted to explain little bit the compound interest, how it is making your savings grow, and even though at the beginning the growth seems very slow this is because the growth with time is exponential and we human beings are not very patient, thus it is important to start early saving small amounts, as snowflakes… in the end you will have a big snowball.
Start saving and see you at the retirement age.”
—–
Final comment: as you may have noticed there several passages when what I say differs from the script. I didn’t learn it by heart. During my first speeches in Toastmasters I tried to do so. Now I am departing from that approach. However, I do write the speech to give it a clear structure, to polish some parts, spot words I may have difficulty in pronouncing (so I can replace them for others) and count the amount of words so I am sure it fits in 5 to 7 minutes (often 7’30”… never more or fellow Toastmasters will start clapping).

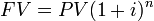

I really love this speech, especially the way in which the formula is explained to make it insightful for us people that get nervous when we meet an exponent!
Thanks!
Knowing exponents well since long ago, I would still get nervious if they’re involved in a default I have with the bank, for instance…
These future sums lose a lot of their attractiveness when you count for inflation.
Pingback: Learning from contests | The Blog by Javier
Pingback: The Unwritten Laws of Finance & Investment | The Blog by Javier